多序列比对
星比对
在序列中选择一个中心序列 (S_c),中心序列的选择算法,在下文详细阐述
将中心序列(S_c)和其余序列进行双序列比对,得到k-1个双序列比对
将k-1个双序列比对进行整合,整合原则“once a gap, always a gap”
例子
S1 ATTGCCATT S2 ATGGCCATT S2 ATGGCCATT S4 ATCTTCTT S5 ACTGACC
1. 建立得分矩阵,取得最大分值的序列做为中心序列。
\[ \sum_{i\neq c}score(s_i, s_c) \]
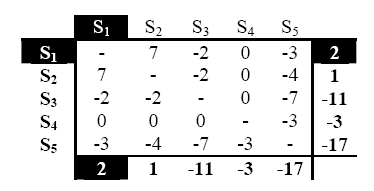
2. 将中心序列与其余序列做比对。

3. 将双序列比对整合到一起,得到MSA。

多核并行
由上文可知,建立得分矩阵选取中心序列是非常耗时的。因此在建立得分矩阵的这个环节,我们可以采取多核并行,加快程序的运行速度。由实际的运行速度来看,并行计算要比单核运行快3.6倍左右(根据电脑的核心数有关,测试电脑的核心数是4核)。
内存优化
针对大型数据集,不能一次将数据读入内存,采取分批次的读取,能有效降低内存的使用。内存消耗由双序列比对和块的大小决定,块最小为一条序列,最大为输入文件的大小。
树比对
建立序列间的距离矩阵,常见的算法有k-tuple、fasta和动态规划等
使用聚类算法,生成指导树,常见的算法有 Neighbor Joining (NJ)、UPGMA等
沿着指导树的顺序进行比对
例子
S1 ATTGCCATT S2 ATGGCCATT S3 ATCTTCTT S4 ACTGACC
1. 生成距离矩阵,并构建指导树
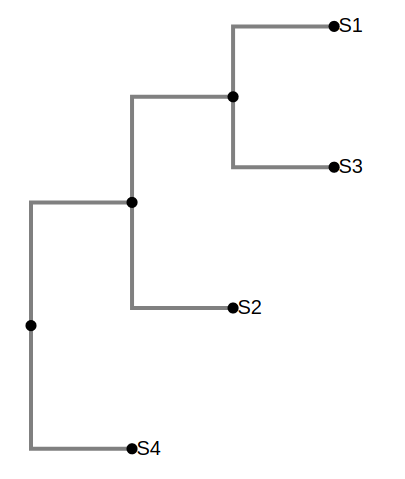
2. 沿着指导树的顺序进行比对
合并S1和S3
S1:AT-TGCCATT
S3:ATCTTC--TT
合并(S1,S3)和S2
S1:AT-TGCCATT
S3:ATCTTC--TT
S2:AT-GGCCATT
合并(S1,S3,S2)和S4
S1:AT-TGCCATT
S3:ATCTTC--TT
S2:AT-GGCCATT
S4:ACTGACC---
比对完成
S1:AT-TGCCATT
S2:AT-GGCCATT
S3:ATCTTC--TT
S4:ACTGACC---
偏序图比对 (Partial Order Multiple Sequence Alignment, PO-MSA/POA)
多序列的有向无环图表示
在 POA 中,首先将每个序列的每个碱基/氨基酸视为一个结点。其次,为了进一步简化 MSA 的表示形式,将原始 MSA 同一列相同/相匹配的结点合并表示。最后,依照节点之间的位置(偏序)关系生成有向边,形成有向无环图(DAG)。
将下述两条序列利用 DAG 表示:
CCGCTTTTCCGC CCGCAAAACCGC
两条序列的 DAG 如下:
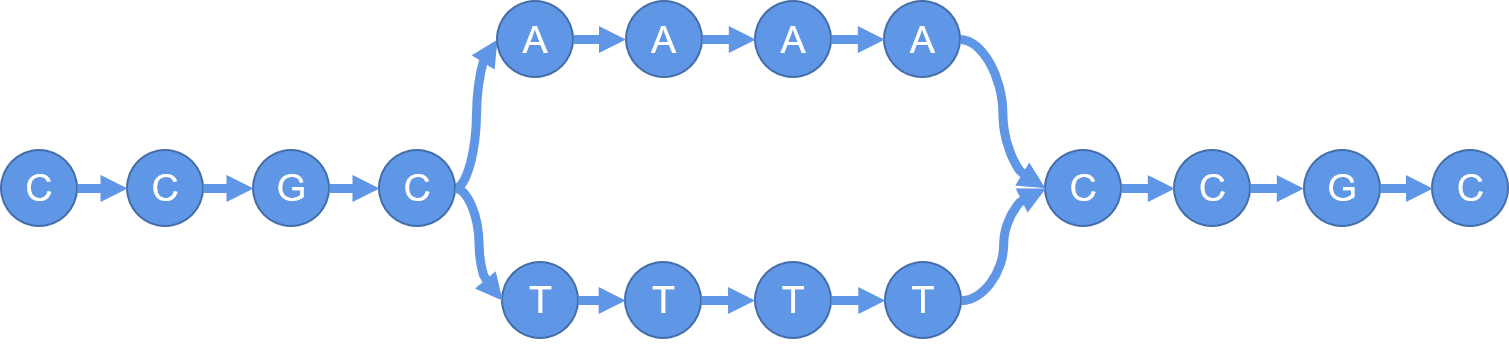
其中,边均为有向边,方向均为从左至右。
基于 POA 求解多序列比对并生成共识序列
共识序列指对于一个 MSA,可以代表 MSA 的大部分性质的序列。在中心星比对中,选取的中心序列被视作共识序列。在 POA 中,为了能更好地代表 MSA,需要生成一条序列作为共识序列。
对于每条序列,利用动态规划与 DAG 进行比对,并合并到 DAG 上
比对完成后,将 DAG 转换成多序列比对结果
依据 DAG 的权重,通过最重束(heaviest bundle)求解最大似然路径。最大似然路径上的点构成共识序列
DAG 与序列的比对
下图展示了一个 DAG 与序列的比对。与序列-序列比对相似,偏序比对可以利用动态规划方法求解,但是需要注意每次比对时,更新矩阵单元的位置。
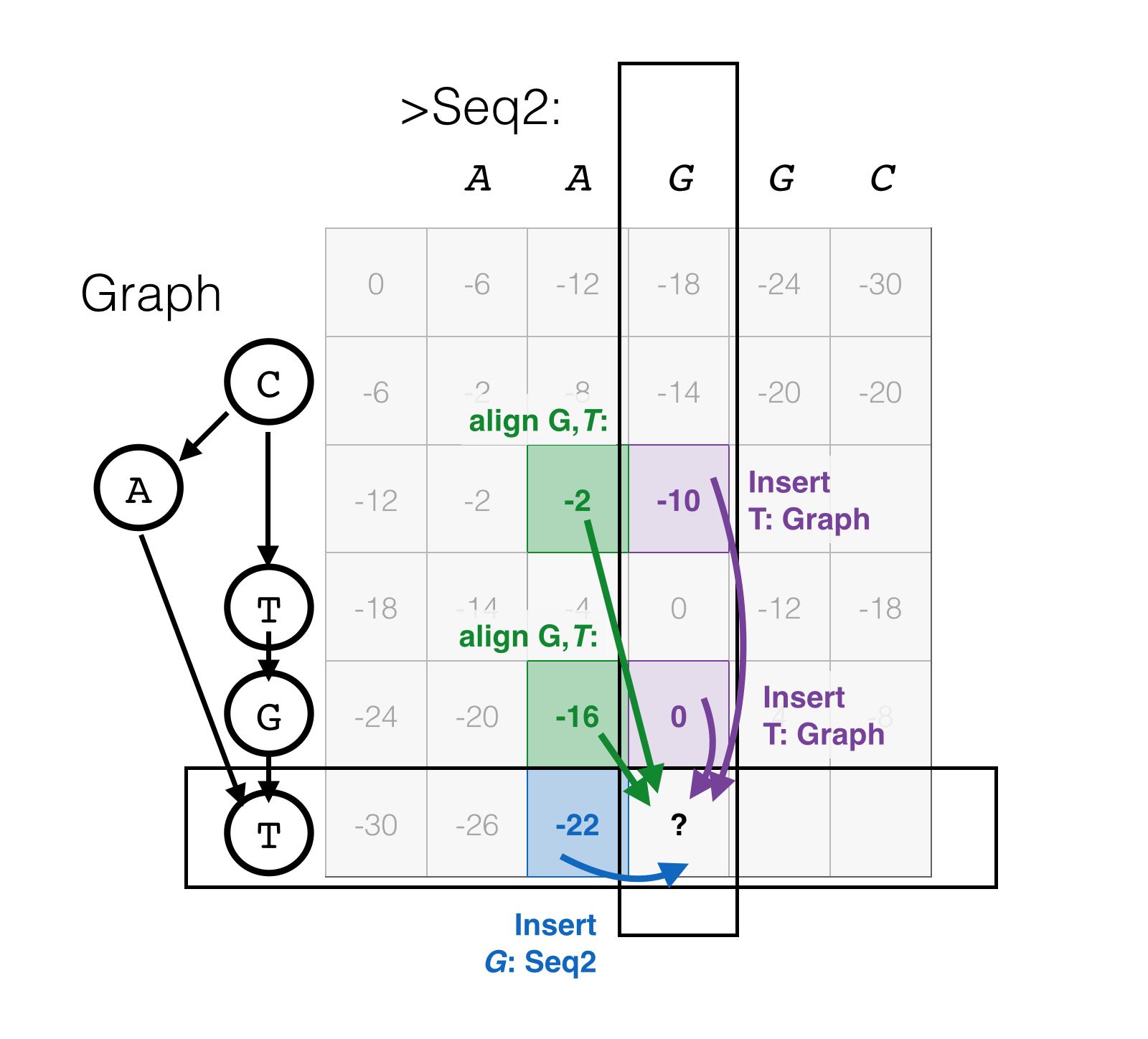
方法实现
前人实现了 K-band + SIMD 优化的偏序图比对:
Ref: Gao, Y., Liu, Y., Ma, Y., Liu, B., Wang, Y., & Xing, Y. (2021). abPOA: an SIMD-based C library for fast partial order alignment using adaptive band. Bioinformatics, 37(15), 2209-2211.